The form is as follows:
minimise $$ f_0(x) $$
subject to $$ f_1(x)\leq b_i, i=1,...,m $$
The optimisation variable of the problem is the following vector:
$$ x=(x_1,...,x_n) $$
The objective function is
$$ f_0:R^n\to R $$
The constraint functions are
$$ f_i:R^n\to R $$
The constrants are
$$ b_1,...,b_m $$
Note that the constrants are the limits or bounds for the constraints.
The smallest objective value among all vectors that satisfy the constraints is the optimal or solution of the problem:
$$ x^* $$
For example,
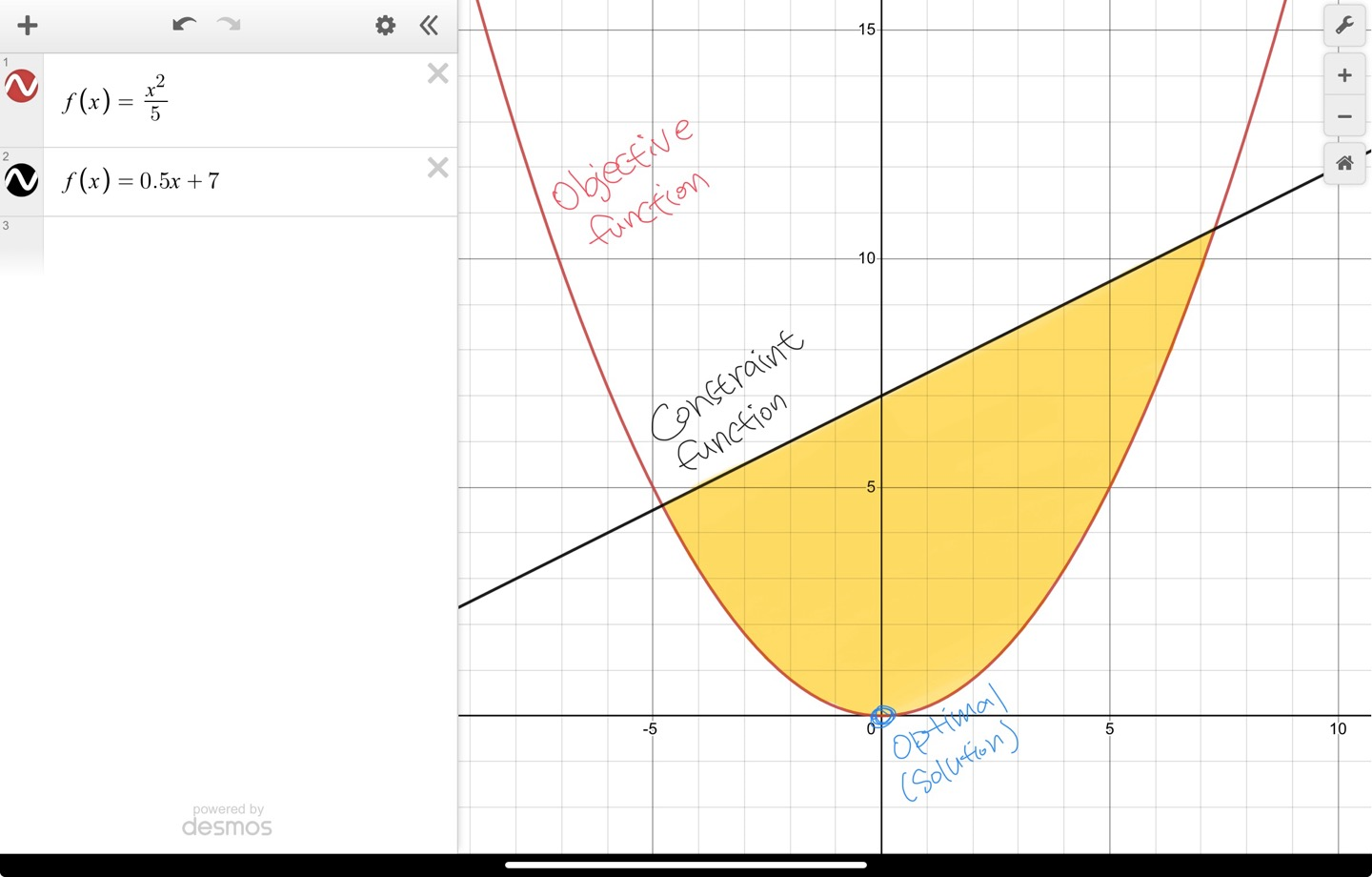
The following convex function (red coloured quadratic function) is
$$ f(x)=2^2/5 $$
The constraint function (black coloured linear function) is
$$ f(x)=0.5x+7 $$
The feasible area is coloured in yellow:
$$ f_1(z) \leq b_1,...,f_m(z) \leq b_m $$
for any z, we have
$$ f_1(z) \leq f_0(x^*) $$
'MachineLearning > Optimisation' 카테고리의 다른 글
| Gradient Vector, Hessian Matrix, and Jacobian Matrix (2) | 2025.07.03 |
|---|---|
| SGD, ADAM, HN ADAM (3) | 2025.06.27 |
| Regularised least squares (RLS) (0) | 2024.01.22 |
| Least-squares problems (0) | 2024.01.16 |