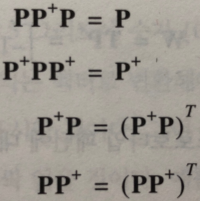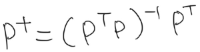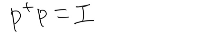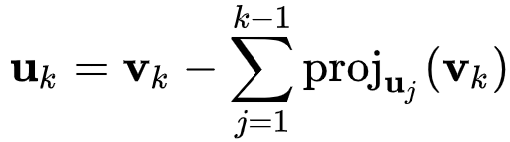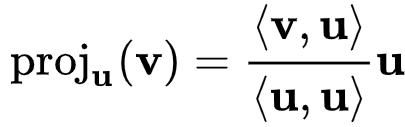Welcome To Sora Park

The De Moivre's formula is:

$$ [r(cos\theta + (\imath *sin\theta ))]^n=r^n((cos * n\theta) + (i * sin * n\theta)) $$

The following two terms are complex numbers, which are the combinations of a Real Number and Imaginary Number:

$$ \imath *sin\theta\ $$

$$ i * sin * n\theta $$

• A Real Number is the type of number: 1.4, 5/8, -2390, 0, for example.
• An Imaginary Number gives a negative result when squared: i^2=-1

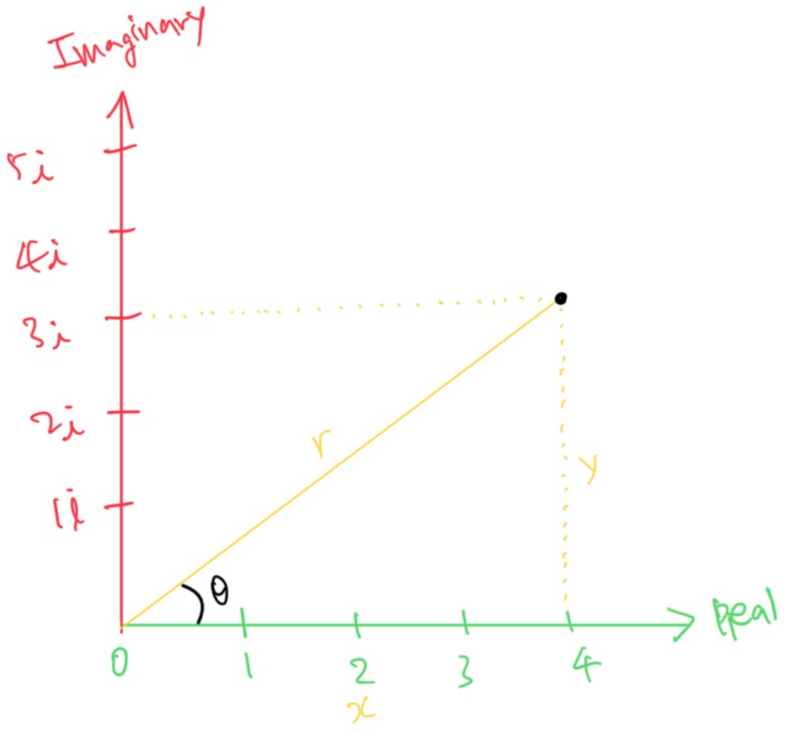
The complex number is

$$ 4 + 3\imath $$

r is

$$ r = \sqrt{4^2+3^2}=\sqrt{25}=5 $$

angle (in radian) is

$$ \Theta =tan^{-1}(y/x)=tan^{-1}(3/4)=0.6435 $$

x is

$$ cos(\theta)=x/r $$

$$ x=r*cos(\theta)=5*cos(0.6435)=4 $$

y is

$$ sin(\theta)=y/r $$

$$ y=r*sin(\theta)=5*sin(0.6435)=3 $$

Here is the common way to write the complex number below:

$$ x+(i*y)=r(cos\theta + (i*(sin\theta)))=r*cis\theta $$

• Note that a combination of cos and sin is often shortened to 'cis'

In the case, therefore, the complex number can be written as follows:

$$ 4+3i=5*cis(0.6435) $$

In the De Moivre's formula,

$$ [r(cos\theta + (\imath *sin\theta ))]^n=r^n((cos * n\theta) + (i * sin * n\theta)) $$

magnitude becomes

$$ r^n $$

angle (in radian) becomes

$$ n\theta $$

In the above case, the De Moivre formula is

$$ (5*cis(0.6435))^2=5^2*cis(2*0.6435)=25*cis(1.287) $$

So, the magnitude is 25 and the angle is 1.287 in radian.

단위 벡터 (unit vector) 는 크기가 1인 벡터를 말한다. 그리고 어떤 벡터를 단위 벡터로 만드는 것을 정규화 (normalisation) 라고 한다.

3차원 벡터를 아래와 같이 정의하면

$$ u=(x,y,z) $$

이 벡터의 크기는 다음과 같이 계산할 수 있다.

$$ \left\| u\right\|=\sqrt{x^2+y^2+z^2} $$

이 벡터를 정규화해서 단위 벡터로 만드는 방법은 벡터의 크기로 각 성분을 나누면 된다.

$$ \hat{u}=\frac{u}{\left\| u\right\|}=
(\frac{x}{\left\| u\right\|}, \frac{y}{\left\| u\right\|}, \frac{z}{\left\| u\right\|})=
(\frac{x}{\sqrt{x^2+y^2+z^2}}, \frac{y}{\sqrt{x^2+y^2+z^2}}, \frac{z}{\sqrt{x^2+y^2+z^2}}) $$

정규화 한 벡터의 크기를 구하면

$$ \left\| \hat{u}\right\|=
\sqrt{(\frac{x}{\sqrt{x^2+y^2+z^2}})^2, (\frac{y}{\sqrt{x^2+y^2+z^2}})^2, (\frac{z}{\sqrt{x^2+y^2+z^2}})^2}=
\sqrt{\frac{x^2+y^2+z^2}{x^2+y^2+z^2}}  $$

이 단위 벡터의 크기는 1이 되는 것을 알 수 있다.

Moore-Penrose inverse of a matrix is the most widely known generalisation of the inverse matrix.

Note that the term 'generalised inverse' is sometimes used as a synonym for pseudopinverse.

History

The common uses of the pseudoinverse are

1. to compute a best-fit least squares solution to a system of linear equations that lacks a solution
2. to find the minimum Euclidean norm solution to a system of linear equations with multiple solutions

The Moore-Penrose pseudoinverse is defined for any matrix and is unique.

The Moore-Penrose pseudoinverse P+ of a matrix P satisfies the following properties:

When P has linearly independent columns, P+ can be computed as

This pseudoinverse is a left inverse that is:

Since P+ is injective, the multiplication of P+ and P is invertible.

• Note that 'injective' means that a function maps distinct elements to distinct outputs. no two elements of P+ map to the same element of P.

When P has linearly independent rows, P+ can be computed as

This is a right inverse as:

Since P+ is surjective, the multiplication of P and P+ is invertible.

• Note that 'surjective' means that a function maps every element of its domain to an element of its codomain. A surjective matrix maps every element of the column space of the matrix to an element of the space.

그람-슈미트 직교성 (Gram-Schmidt orthogonalization) 이해를 위한 개념

• 내적 (inner product): 두 벡터의 닮음 정도 (직각으로 갈수록 0에 가까워지고, 반대 방향의 경우 음수)
• 투영 (projection): 벡터 A에서 벡터 B로 직각 내렸을 때 (빛을 쏘면 어두워지는 영역을 생각하면 됨) A와 B가 맞닿는 벡터가 vector projection, 그 벡터의 길이가 scalar projection
• 놈 (norm): 기준점에서 한 벡터까지의 거리 (길이) 로서, 여러 놈이 있음
  • L0 norm: 길이를 나타내는 norm 의 개념이 아니라 vector 값 중 0이 아닌 값 개수
  • L1 norm: Manhattan distance 로 계산된 값
  • L2 norm: Euclidean distance 로 계산된 값으로, 같은 좌표가 주어졌을 때 L1 norm 보다 길이가 긴 편
  • L-infinity norm: max norm 이라고 불리며 vector 값 중 절대값이 가장 큰 값

두 벡터의 내적이 0 일 경우, 두 벡터는 직교한다.

벡터 A에 대한 직교 벡터 B를 구하는 방법은 벡터 A에서 벡터 A를 투영한 벡터를 빼면 된다.

위 그림은 연속된 벡터셋이 주어졌을 때 벡터 (Vk) 마다 직교하는 벡터 (Uk) 를 구하는 방법을 나타낸다.

식에 주어진 projection operator 는 위 그림과 같이 나타낼 수 있다. <> 표현은 내적을 뜻한다. 예를 들어 <U, U> 는 벡터 U와 벡터 U의 내적을, <V, U> 는 벡터 V와 벡터 U의 내적을 나타낸다. Uk와 무관한 'U'의 뜬금 없는 등장은 이 식이 연속된 벡터가 주어졌을 때 순서대로 직교성을 파악하기 위한 전개식으로, Uj의 j는 k-1으로 보면 된다.

직교화를 기하학적으로 생각하면 벡터 U 자신의 내적은 닮다 못해 아예 같이 때문에 최대 값이 될 거고, 이 값을 벡터 V와 벡터 U의 닮음 정도에 나누면 그 비율을 구할 수 있다. 이 비율을 벡터 U와 곱하면 비율만큼 길이에 변화가 생긴 벡터 U'가 나오게 되고, 이 U'가 바로 벡터 V와 직교하는 벡터가 된다.

그람-슈미트 직교화의 전 과정은 아래와 같다.

첫번째 직교벡터는 대상벡터로 지정하고, 두번째부터 projection operator 를 이용해 각 직교벡터를 구하면 된다.

예를 들어, 기저 벡터 집합 3개가 있다.

$$ y_1=\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}, y_2=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}, y_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix} $$

그람-슈미트 직교화를 이용해 직교 집합을 찾으려면

1단계:

$$ v_1=y_1=\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix} $$

2단계:

$$ v_2=y_2-\frac{v_1^Ty_2}{v_1^Tv_1}v_1=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}-\frac{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}}{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}-\begin{bmatrix}
\frac{1}{3} \\ \frac{1}{3} \\ \frac{1}{3}
\end{bmatrix}=\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix} $$

3단계:

$$ v_3=y_3-\frac{V_1^Ty_3}{v_1^Rv_1}v_1-\frac{v_2^Ty_3}{v_2^Tv_2}v_2 $$

$$ v_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}-\frac{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}}{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}-\frac{\begin{bmatrix}
2/3 & -1/3 & -1/3 \\
\end{bmatrix}\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}}{\begin{bmatrix}
2/3 & -1/3 & -1/3 \\
\end{bmatrix}\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix}}\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix} $$

$$ v_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}-\begin{bmatrix}
1/3 \\ 1/3 \\ 1/3
\end{bmatrix}-\begin{bmatrix}
-1/3 \\ 1/6 \\ 1/6
\end{bmatrix}=\begin{bmatrix}
0 \\ 1/3 \\ -1/3
\end{bmatrix} $$

이렇게 3단계로 구할 수 있다.