Welcome To Sora Park

Hopcroft-Karp algorithm (sometimes more accurately called the Hopcroft-Karp-Karzanov algorithm) is an algorithm for solving the maximum matching problem in a bipartite graph. This algorithm produces a maximum cardinality matching as output and runs in O(E√V) time in the worst case, where E is set of edges in the graph and V is set of vertices of the graph.

Bi-partite graph (also known as bigraph)

A graph G(V,E) is called a bipartite graph. V and E are usually called the parts of the graph.

If the set of vertices V can be partitioned in two no-empty disjoint sets V1 and V2 in such a way that each edge e in G has one endpoint in V1 and another endpoint in V2.

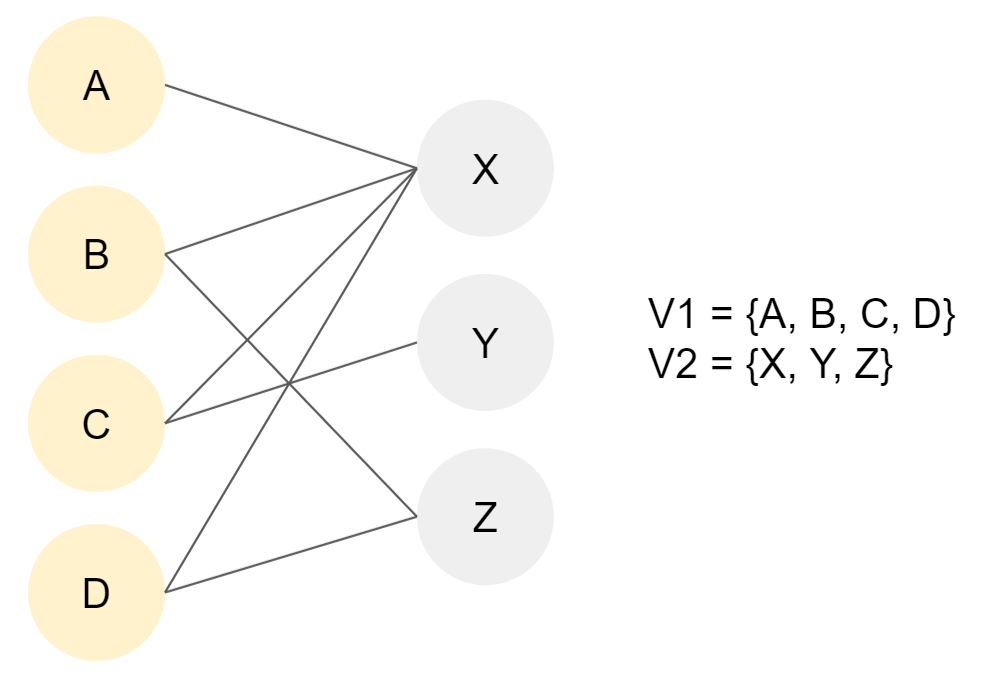
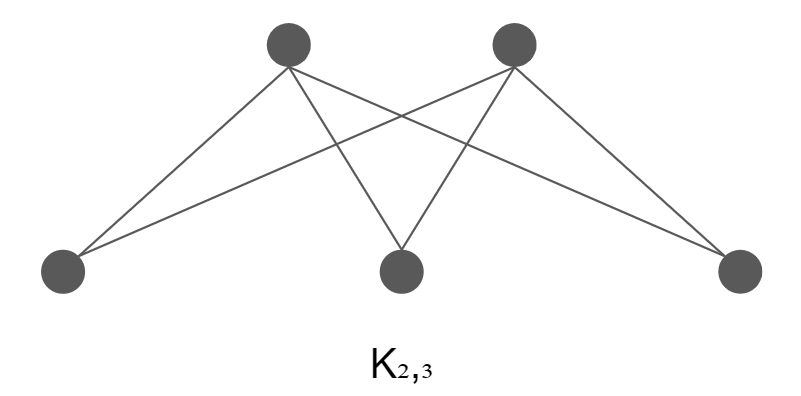
Complete bipartite graph

If each vertex in A is adjacent to all the vertices in B, then the graph is a complete bipartite graph and gets a special name: Km,n, where |A| = m and |B| = n.

Matching

A set of pairwise non-adjacent edges, none of which are loops; that is, no two edges share a common endpoint.

• A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching.
• Otherwise, the vertex is unmatched.

A matching in a bipartite graph is a set of the edges chosen in such a way that no two edges share an endpoint.

Maximum matching (also known as Maximum-Cardinality Matching)

• A maximum matching is a matching of maximum size (maximum number of edges).
• If any edge is added, it is no longer matching.

For example, a maximum of five people can get jobs in the following graph of an assignment of jobs to applicants.

Hopcroft-Karp algorithm is often outperformed by Breadth-First and Depth-First approaches to finding augmenting paths.

Augmenting paths

Given a matching M, an augmenting path is an alternating path that starts from and ends on free vertices.

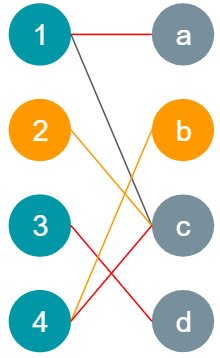
• 2 and b are free vertices.
• A walk from 2 to c and a walk from 4 to b are augmented paths.

How Hopcroft-Karp algorithm works

• Define two sets of vertices from the bipartition of G, U and V, with an equal number of nodes.
• The matchings, or set of edges, between nodes in U and nodes in V, is called M.

The algorithm runs in phases mode up of the following steps:

1. Use a BFS to find augmenting paths.
   If partitions the vertices of the graph into layers of matching and not matching U.
   For the search, start with the free nodes in U.
   This forms the first layer of the partitioning.
   The search finishes at the first layer k where one or more free nodes in V are reached.
2. The free nodes in V are added to a set called F.
   This means that any node added to F will be the ending node of an augmenting pathㅡand a shortest augmenting path at that since the BFS finds the shortest paths.
3. Once an augmenting path is found, a DFS is used to add augmenting paths to current matching M.
   At any given layer, the DFS will follow edges that lead to an unused node from the previous layer.
   Paths in the DFS tree must be alternating paths (switching between matched and unmatched edges).
   Once the algorithm finds an augmenting path that uses a node from F, the DFS moves on to the next starting vertex.

2021.09.03 - [Algorithms] - Breadth-first, Depth-first searches (BFS/DFS)

Example

Observe the graph with edges but no assigned matchings.

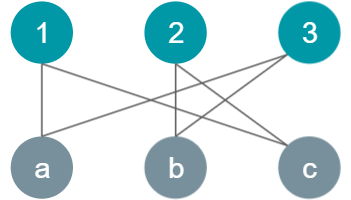
Step 1: Perform BFS starting at all the numeric vertices without a match. Pick any unmatched leaf and go all the way back to a root using DFS. Match the leaf to the root.

• Match a to 1.
• Delete all the instances of 1 and a found in the trees.

Step 2: Repeat the process to find the next matching.

• Match b to 2.
• Delete b from the tree spanning from 3.
• In this iteration, 1 is matched to a, 2 is matched to b, and 3, along with c, is left without a match.

Step 3: Since 3 is left without a match, perform BFS starting from 3 in order to find a matching or assert that the current matching is already optimal.

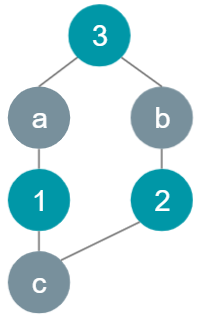
Perform DFS once again from the unmatched leaf all the way to the root.

• DFS finds a path from c to 1, to 1, and terminates at 3.

Step 4: Augment the path by switching the edges that are matched with those that are unmatched.

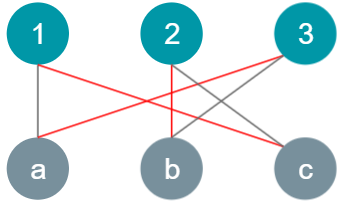
• New 1 is matched with c and 3 is matched with a.
• This produces the maximal matching between numbers and letters in G.

Breadth-first search (BFS)

BFS is a traversing algorithm that starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory is needed to keep track of the child nodes that were encountered but not yet explored.

The traversing process is as follows:

Pseudocode

BFS(G, root) is
	let Q be a queue
    label root as explored
    Q.enqueue(root) // insert a tree root in queue until every neighbour vertices are marked
    while Q is not empty do:
    	v := Q.dequeue() // remove a to-be-visited vertex from queue
        if v is the goal then
        	return v
        for all edges from v to w in G.adjacentEdges(v) do:
        	if w is not labelled as explored then
            	label w as explored
                Q.enqueue(w) // store w in Q if it's not visited
        end for
    end while
end

Depth-first search (DFS)

DFS is a traversing algorithm that starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

The traversing process is as follows:

Pseudocode

DFS(G,v) // v is the vertex where the search starts
	Stack S := {}; // start with an empty stack
    for each vertex u, set visited[u] := false
    	push S, v;
        while S is not empty do:
        	u := pop S;
            if u is not visited then
            	visited[u] := true;
                for each unvisited neighbout w of u
                	push S, w;
                end for
         end while
     end for
end

Example

The number of vertices: 4

The number of edges: 5

Start node: 1

#include <iostream>
#include <queue>

#define MAX_VAL 1001

int N, M, V;
int mat[MAX_VAL][MAX_VAL];
bool visited[MAX_VAL];

using namespace std;
void dfs(int v)
{
    printf("%d, ", v);
    visited[v] = true;
    for (int i = 1; i <= N; i++)
    {
        if (visited[i] || mat[v][i] == 0)
            continue;
        dfs(i);
    }
}

void bfs(int v)
{
    queue<int> q;
    q.push(v);
    visited[v] = true;
    while (!q.empty())
    {
        v = q.front();
        printf("%d, ", q.front());
        q.pop();
        for (int i = 1; i <= N; i++)
        {
            if (visited[i] || mat[v][i] == 0)
                continue;
            q.push(i);
            visited[i] = true;
        }
    }
}

int main()
{
    int x, y;
    cin >> N >> M >> V;
    for (int i = 0; i < M; i++)
    {
        cin >> x >> y;
        mat[x][y] = mat[y][x] = 1;
    }
    memset(visited, false, sizeof(visited));
    dfs(V);
    prinft("\n");
    memset(visited, false, sizeof(visited));
    bfs(V);
}

Complexity

• |V| is the number of vertices
• |E| is the number of edges