그람-슈미트 직교성 (Gram-Schmidt orthogonalization) 이해를 위한 개념
- 내적 (inner product): 두 벡터의 닮음 정도 (직각으로 갈수록 0에 가까워지고, 반대 방향의 경우 음수)
- 투영 (projection): 벡터 A에서 벡터 B로 직각 내렸을 때 (빛을 쏘면 어두워지는 영역을 생각하면 됨) A와 B가 맞닿는 벡터가 vector projection, 그 벡터의 길이가 scalar projection
- 놈 (norm): 기준점에서 한 벡터까지의 거리 (길이) 로서, 여러 놈이 있음
- L0 norm: 길이를 나타내는 norm 의 개념이 아니라 vector 값 중 0이 아닌 값 개수
- L1 norm: Manhattan distance 로 계산된 값
- L2 norm: Euclidean distance 로 계산된 값으로, 같은 좌표가 주어졌을 때 L1 norm 보다 길이가 긴 편
- L-infinity norm: max norm 이라고 불리며 vector 값 중 절대값이 가장 큰 값
두 벡터의 내적이 0 일 경우, 두 벡터는 직교한다.
벡터 A에 대한 직교 벡터 B를 구하는 방법은 벡터 A에서 벡터 A를 투영한 벡터를 빼면 된다.
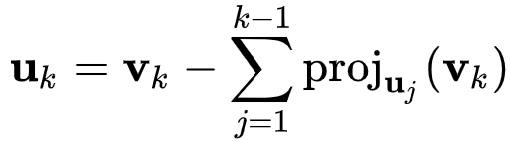
위 그림은 연속된 벡터셋이 주어졌을 때 벡터 (Vk) 마다 직교하는 벡터 (Uk) 를 구하는 방법을 나타낸다.
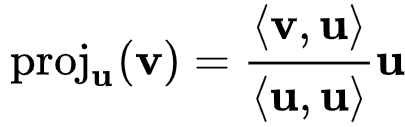
식에 주어진 projection operator 는 위 그림과 같이 나타낼 수 있다. <> 표현은 내적을 뜻한다. 예를 들어 <U, U> 는 벡터 U와 벡터 U의 내적을, <V, U> 는 벡터 V와 벡터 U의 내적을 나타낸다. Uk와 무관한 'U'의 뜬금 없는 등장은 이 식이 연속된 벡터가 주어졌을 때 순서대로 직교성을 파악하기 위한 전개식으로, Uj의 j는 k-1으로 보면 된다.
직교화를 기하학적으로 생각하면 벡터 U 자신의 내적은 닮다 못해 아예 같이 때문에 최대 값이 될 거고, 이 값을 벡터 V와 벡터 U의 닮음 정도에 나누면 그 비율을 구할 수 있다. 이 비율을 벡터 U와 곱하면 비율만큼 길이에 변화가 생긴 벡터 U'가 나오게 되고, 이 U'가 바로 벡터 V와 직교하는 벡터가 된다.
그람-슈미트 직교화의 전 과정은 아래와 같다.
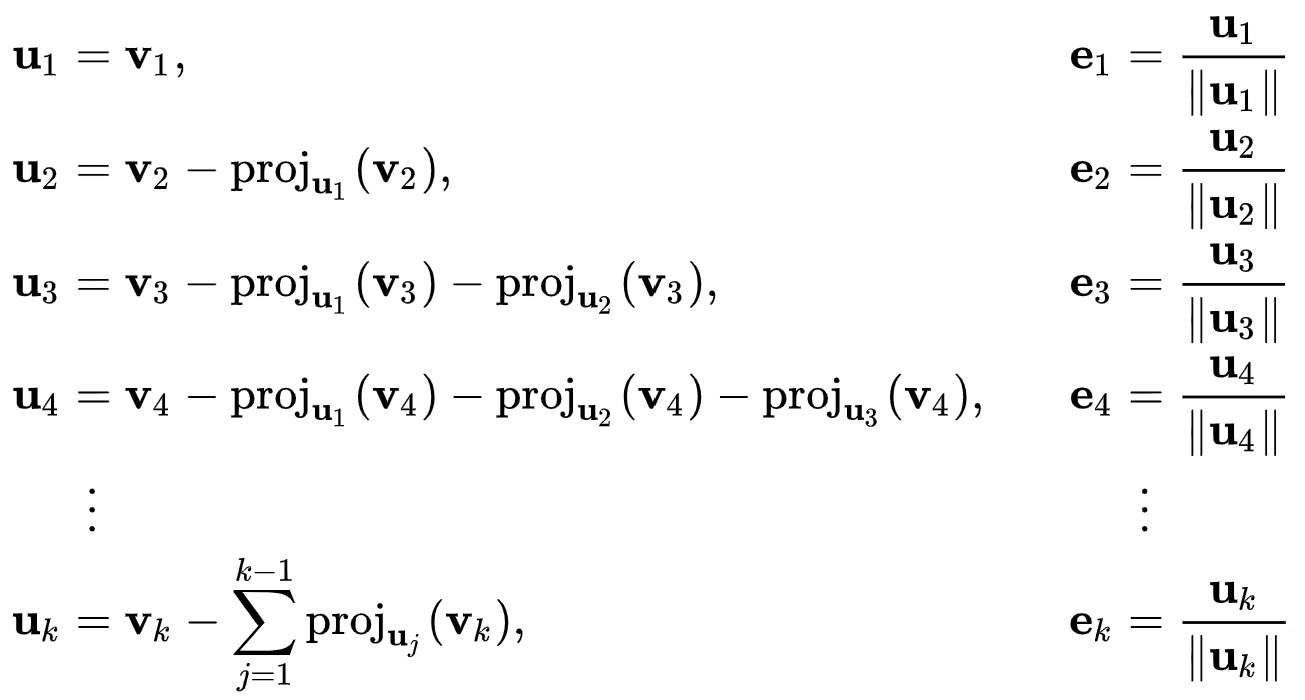
첫번째 직교벡터는 대상벡터로 지정하고, 두번째부터 projection operator 를 이용해 각 직교벡터를 구하면 된다.
예를 들어, 기저 벡터 집합 3개가 있다.
$$ y_1=\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}, y_2=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}, y_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix} $$
그람-슈미트 직교화를 이용해 직교 집합을 찾으려면
1단계:
$$ v_1=y_1=\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix} $$
2단계:
$$ v_2=y_2-\frac{v_1^Ty_2}{v_1^Tv_1}v_1=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}-\frac{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}}{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}-\begin{bmatrix}
\frac{1}{3} \\ \frac{1}{3} \\ \frac{1}{3}
\end{bmatrix}=\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix} $$
3단계:
$$ v_3=y_3-\frac{V_1^Ty_3}{v_1^Rv_1}v_1-\frac{v_2^Ty_3}{v_2^Tv_2}v_2 $$
$$ v_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}-\frac{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}}{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}-\frac{\begin{bmatrix}
2/3 & -1/3 & -1/3 \\
\end{bmatrix}\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}}{\begin{bmatrix}
2/3 & -1/3 & -1/3 \\
\end{bmatrix}\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix}}\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix} $$
$$ v_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}-\begin{bmatrix}
1/3 \\ 1/3 \\ 1/3
\end{bmatrix}-\begin{bmatrix}
-1/3 \\ 1/6 \\ 1/6
\end{bmatrix}=\begin{bmatrix}
0 \\ 1/3 \\ -1/3
\end{bmatrix} $$
이렇게 3단계로 구할 수 있다.
'Mathematics' 카테고리의 다른 글
| Vector Normalisation 벡터 정규화 (0) | 2023.10.24 |
|---|---|
| Moore-Penrose inverse 무어-펜로즈 의사역행렬 (0) | 2023.09.13 |
| Pascal's rule (0) | 2021.09.02 |
| Combinations with repetition (0) | 2021.08.26 |
| Permutation with repetition (0) | 2021.08.26 |