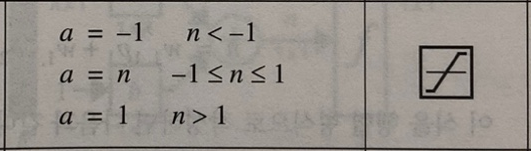
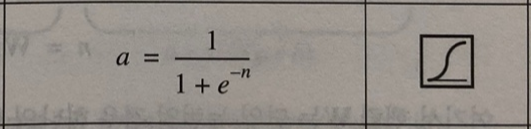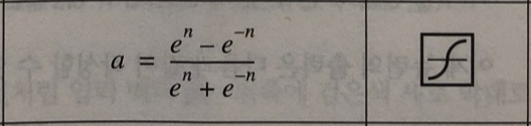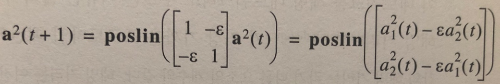Models that assign probabilities to upcoming words, or sequences of words in general, are called language models (LMs).
- Predicting upcoming words turns out that the large language models that revolutionised modern NLP are trained just by predicting words.
Why does it matter what the probability of a sentence is or how probable the next word is?
- In many NLP applications, we can use the probability as a way to choose a better sentence or word over a less-appropriate one.
Language models can also help in augmentative and alternative communication (AAC) systems.
- People often use such AAC devices if they are physically unable to speak or sign but can instead use eye gaze or other specific movements to select words from a menu.
- Word prediction can be used to suggest likely words for the menu.
N-gram language model
- An n-gram is a sequence of n words:
- A 2-gram (bigram) is a two-word sequence of words like "please turn", "turn your", or "your homework".
- A 3-gram (trigram) is a three word sequence of words like "please turn your", or "turn your homework".
- The word 'n-gram' is also used to mean a probabilistic model that can estimate the probability of a word given the n-1 previous words, and thereby also to assign probabilities to entire sequences.
Suppose the history h is "its water is so transparent that" and we want to know the probability that the next word is "the":
P(the | its water is so transparent that)
One way to estimate this probability is from relative frequency counts:
- Take a very large corpus, count the number of times we see "its water is so transparent that", and count the number of times this is followed by "the'.
Out of the times we saw the history h, how many times was it followed by the word w, as follows:
P(the | its water is so transparent that) = C(its water is so transparent that the) / C(its water is so transparent that)
To represent the probability of a particular random variable
$$ X_i $$
taking on the value "the" or
$$ P(X_i="the") $$
we will use the simplication
$$ P(the) $$
To compute probabilities of entire sequences like
$$ P(X_n|X_{1:n-1}) $$
One things we can do is decompose this probability using the chain rule of probability:
$$ P(X_1...X_n)=P(X_1)P(X_2|X_1)P(X_3|X_{1:2})...P(X_n|X_{1:n-1}) $$
$$ = \prod_{k=1}^{n}P(X_k|X_{1:k-1}) $$
Applying the chain rule to words, we get:
$$ P(w_{1:n})=P(w_1)P(w_2|w_1)P(w_3|w_{1:2})...P(w_n|w_{1:n-1}) $$
$$ =\prod_{k=1}^{n}P(w_k|w_{1:k-1}) $$
The chain rule shows the linke between computing the joint probability of a sequence and computing the conditional probability of a word given previous words.
- We could estimate the joint probability of an entire sequence of words by multiplying together a number of conditional probabilities.
We can't just estimate by counting the number of times every word occurs following every long string, because language is creative and any particular context might have never occurred before.
The intuition of the n-gram model is that instead of computing the probability of a word given its entire history, we can approximate the history by just the last few words.
- For example, the bigram model approximates the probability of a word given all the previous words by using only the conditional probability of the preceding word.
- Instead of computing the probability P(the | Walden Pond's water is so transparent that),
we approximate it with the probability P(the | that)
- Instead of computing the probability P(the | Walden Pond's water is so transparent that),
- When we use a bigram model to predict the conditional probability of the next word, we are thus making the following approximation:
$$ P(w_n|w_{1:n-1})\approx P(w_n|w_{n-1}) $$
The assumption that the probability of a word depends only on the previous word is called a Markov assumption.
- Markov models are the class of probabilistic models that assume we can predict the probability of some future unit without looking too far into the past.
A general equation for a n-gram approximation to the conditional probability of the next word in a sequence:
$$ P(w_n|w_{1:n-1})\approx P(w_n|w_{n-N+1:n-1}) $$
※ N means the n-gram size (N=2 means bigrams and N=3 means trigrams)
An intuitive way to estimate probabilities is called maximum likelihood estimation (MLE).
- We get the MLE estimate for the parameters of an n-gram model by getting counts from a corpus, and normalising the counts so that they lie between 0 and 1.
To compute a particular bigram probability of a word
$$ w_n $$
given a previous word
$$ w_{n-1} $$
we'll compute the count of the bigram
$$ C(w_{n-1}w_n) $$
and normalise by the sum of all the bigrams that share the same first word
$$ w_{n-1} $$
The computation is:
$$ P(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)}{\sum _wC(w_{n-1}w)} $$
The sum of all bigram counts that start with a given word
$$ W_{n-1} $$
must be equal to the unigram for that word, so the simplified equation is as follows:
$$ P(w_n|w_{n-1})=\frac{C(w_{n-1}w_n)}{C(w_{n-1})} $$
Language model probabilities are always represented and computed in log format as log probabilities.
- Since probabilities are less than or equal to 1, the more probabilities we multiply together, the smaller the product becomes.
By using log probabilities instead of raw probabilities, we get numbers that are not as small.
- Adding in log space is equivalent to multiply in linear space, so we combine log probabilities by adding them.
$$ P_1\times P_2\times P_3\times P_4=exp(log{P_1}+log{P_2}+log{P_3}+log{P_4}) $$
The result of doing all computation and storage in log space is that we only need to convert back into probabilities if we need to report them at the end; then we can just take the exp of the logprob!
Evaluating language models
- Extrinsic evaluation is the end-to-end evaluation (often very expensive!)
- Intrinsic evaluation measures the quality of a model independent of any application
- Perplexity (sometimes abbreviated as PP or PPL): the standard intrinsic metric for measuring language model performance, both for simple n-gram language models and for the more sophisticated neutral large language models.
In order to evaluate any machine learning model, at least three distinct data sets are needed:
- Training set is used to learn the parameters of the model
- Development test set (or devset) is used to see how good the model is by testing on the test
- Test set is used to evaluate the model → held-out set of data, not overlapping with the training set
Given two probabilistic models, the better model is the one that has a tighter fit to the test data or that better predicts the details of the test data, and hence will assign a higher probability to the test data.
The perplexity of a language model on a test set is the inverse probability of the test set (one over the probability of the test set), normalised by the nubmer of words. For this reason, it's sometimes called the per-word perplexity.
For a test set
$$ W=w_1w_2...w_N $$
$$ perplexity(W)=P(w_1w_2...w_N)^{-\frac{1}{N}} $$
$$ =\sqrt[N]{\frac{1}{P(w_1w_2...w_N)}} $$
Or we can use the chain rule to expand the probability of W:
$$ \sqrt[N]{\prod_{i=1}^{N}\frac{1}{P(w_i|w_1...w_{i-1})}} $$
- Because of the inverse, the higher the probability of the word sequence, the lower the perplexity.
→ Thus the lower the perplexity of a model on the data, the better the model, and minimising perplexity is equivalent to maximising the test set probability according to the language model.
Perplexity can also be thought of as the weighted average branching factor of a language.
- The branching factor of a language is the number of possible next words that can follow any word.
If we have an artificial deterministic language of integer numbers whose vocabulary consists of the 10 digits, in which any digit can follow any other digit, then the branching factor of that language is 10.
Suppose that each of the 10 digits with exactly equal probability:
$$ P=\frac{1}{10} $$
Imagine a test string of digits of length N, and again, assume that in the training set all the digits occurred with equal probability. The perplexity will be
$$ perplexity(W)=P(w_1w_2...w_N)^{-\frac{1}{N}}=(\frac{1}{10}^N)^{-\frac{1}{N}}=\frac{1}{10}^{-1}=10 $$
'NaturalLanguageProcessing > Concept' 카테고리의 다른 글
| (w08) Vector semantics and embeddings (0) | 2024.05.27 |
|---|---|
| (w07) Lexical semantics (0) | 2024.05.22 |
| (w04) Regular expression (0) | 2024.04.30 |
| (w03) Text processing fundamentals (0) | 2024.04.24 |
| (w02) NLP evaluation -basic (0) | 2024.04.17 |