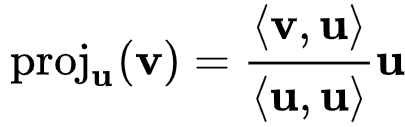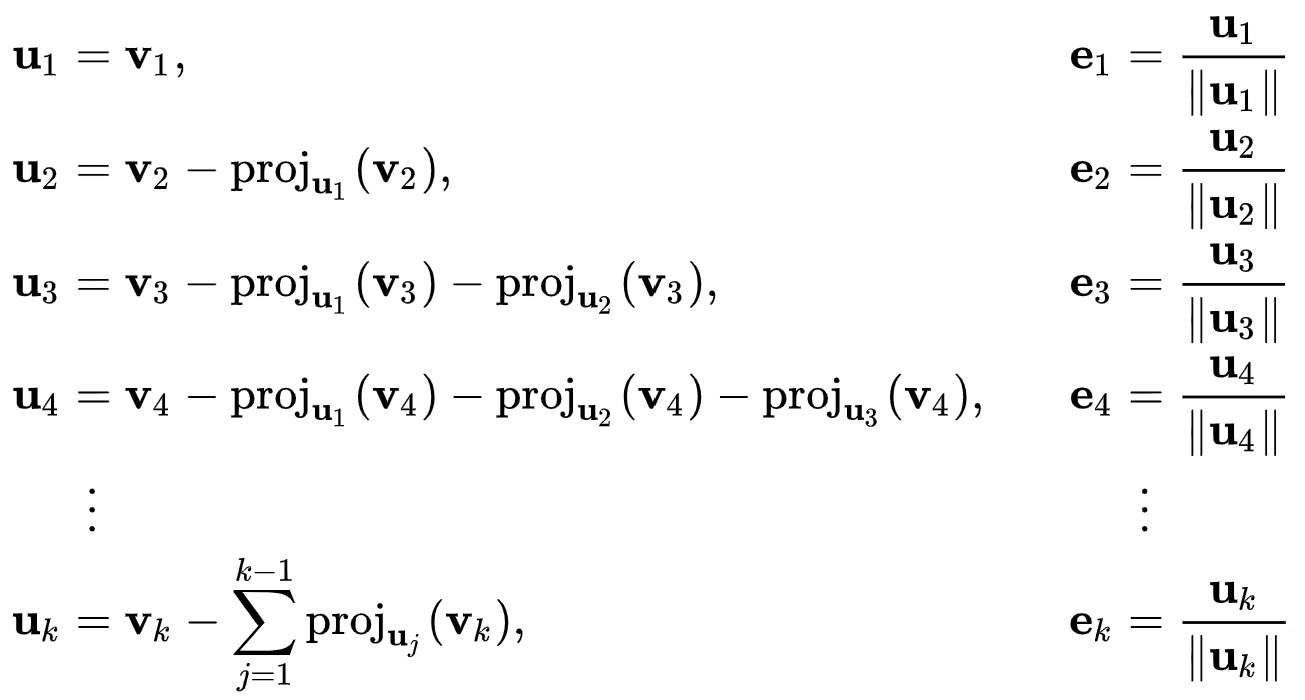Welcome To Sora Park

헵 규칙 (Hebb rule) 은 최초의 신경망 학습 규칙 중 하나로, 1949년 도널드 헵 (Donald O. Hebb) 이 뇌의 시냅스 변형 메커니즘으로 제안한 이후로 인공 신경망 훈련에 사용되고 있다.

당시 헵이 집필한 'The Organization of Behavior' 책에는 헵 학습으로 알려진 가정 (공리) 이 있다.

세포 A의 축삭이 세포 B를 자극하기에 충분히 가깝고 B를 발화하는 데 반복적 또는 지속적으로 참여할 때, 한쪽 또는 양쪽 세포에 일종의 성장 과정이나 신진대사의 변화가 일어남으로써 B를 발화하는 세포 중 하나로서 A의 효율이 올라간다.

헵 학습 규칙은 다양한 신경망 구조와 결합해서 사용할 수 있다. 예를 들어 선형 연상 메모리 (linear associator) 가 있다.

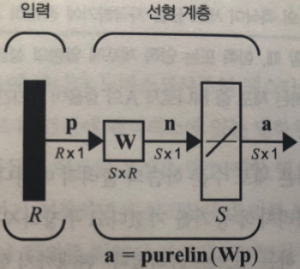
이는 연상 메모리 (associative memory) 라고 하는 신경망 종류의 한 예로, 연상 메모리의 작업은 프로토타입 입력/출력 벡터의 Q개 쌍을 학습하는 것이다.

$$ \{p_1,t_1\}, \{p_2,t_2\}, ... , \{p_Q,t_Q\} $$

네트워크가 입력 p를 받으면 출력 t를 생성해야 하는데, 입력이 바뀌면 출력도 약간 바뀌어야 한다.

시냅스 양쪽에 있는 두 뉴런이 동시에 활성화되면 시냅스의 강도는 증가하게 될 것이다.

• 위 그림에서 입력 p와 출력 a의 연결 (시냅스) 은 가중치 w이다.

헵의 가정은 양의 p가 양의 a를 생성한다면 w가 증가해야 한다는 것을 의미한다. 수학적 해석은 아래와 같다.

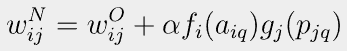
• p는 q번째 입력 벡터의 j번째 요소
• a는 q번째 입력 벡터가 네트워크에 제시될 때 네트워크 출력의 i번째 요소
• 알파는 양의 상수이며, 학습률 (learning rate) 이라고 부름

이 식은 가중치 w의 변화가 시냅스 양쪽의 활성 함수의 곱에 비례한다는 사실을 말해준다.

참고로 이 식에 정의된 헵 규칙은 비지도 학습 (unsupervised learning) 규칙이므로, 목표 출력에 관련된 정보가 필요 없다. 지도 (supervised) 헵 규칙에서는 실제 출력을 목표 출력으로 대체할 수 있다.

이 방법은 알고리즘에게 '네트워크가 현재 하고 있는 것'이 아닌 '네트워크가 해야만 하는 것'을 알려준다.

• t는 q번째 목표 벡터 t의 i번째 요소
• 학습률은 1로 설정

벡터 표기법은 아래와 같다.

$$ W^N=W^O+t_qp_q^T $$

가중치 행렬을 0으로 초기화하고 Q개의 입력/출력 쌍을 한번에 적용하면 아래와 같이 작성할 수 있다.

$$ W=t_1p_1^T+t_2p_2^T+ ... +t_QP_Q^T=\sum_{q=1}^{Q}t_qp_q^T $$

이 식은 행렬 방식으로 표현될 수 있다.

$$ W=\begin{bmatrix}
t_1 & t_2 & ... & t_Q \\
\end{bmatrix}\begin{bmatrix}
p_1^T \\ p_2^T \\ ... \\ p_Q^T
\end{bmatrix}=TP^T $$

여기서

$$ T=\begin{bmatrix}
t_1 & t_2 & ... & t_Q \\
\end{bmatrix}, P=\begin{bmatrix}
p_1 & p_2 & ... & p_Q \\
\end{bmatrix} $$

선형 연상 메모리에 대한 헵 학습의 성능 분석 시 프로토타입 벡터 (p_q) 가 직교하면서 단위 길이를 갖는 정규직교 (orthonormal) 인 경우와 단위 길이를 갖지만 직교하지 않는 경우를 나눠서 살펴볼 수 있다.

1. 정규직교인 경우:
   p_k 가 네트워크 입력이면 네트워크 출력은 다음과 같이 계산된다.
   $$ a=Wp_k=(\sum_{q=1}^{Q}t_qp_q^T)p_k=\sum_{q=1}^{Q}t_q(p_q^Tp_k) $$
   p_q 가 정규직교이기 때문에 다음과 같이 된다.
   $$ (p_q^Tp_k)=1, q=k $$
   $$ (p_q^Tp_k)=0, q!=k $$
   Identity matrix 가 되기 때문에 네트워크 출력은 다음과 같이 간단하게 작성될 수 있다.
   $$ a=Wp_k=t_k $$
2. 단위 길이이지만, 직교가 아닌 경우:
   벡터가 직교하지 않기 때문에 네트워크는 정확한 출력을 생성하지 않을 것이며, 오차의 크기는 프로토타입 입력 패턴 사이에 상관 관계의 크기에 따라 달라진다.
   $$ a=Wp_k=t_k+\sum_{q!=k}^{}t_q(p_q^Tp_k) $$
   우항의 시그마는 오차를 나타낸다.

예제 1) 입력 벡터가 정규직교일 때

$$ p_1=\begin{bmatrix}
0.5 \\ -0.5 \\ 0.5 \\ -0.5
\end{bmatrix}, t_1=\begin{bmatrix}
1 \\ -1
\end{bmatrix}  $$

$$ p_2=\begin{bmatrix}
0.5 \\ 0.5 \\ -0.5 \\ -0.5
\end{bmatrix}, t_2=\begin{bmatrix}
1 \\ 1
\end{bmatrix} $$

가중치 행렬:

$$ W=TP^T=\begin{bmatrix}
1 & 1 \\
-1 & 1 \\
\end{bmatrix}\begin{bmatrix}
0.5 & -0.5 & 0.5 & -0.5 \\
0.5 & 0.5 & -0.5 & -0.5 \\
\end{bmatrix}=\begin{bmatrix}
1 & 0 & 0 & -1 \\
0 & 1 & -1 & 0 \\
\end{bmatrix} $$

각각의 프로토타입 입력에 대한 가중치 행렬 테스트 결과:

$$ Wp_1=\begin{bmatrix}
1 & 0 & 0 & -1 \\
0 & 1 & -1 & 0 \\
\end{bmatrix}\begin{bmatrix}
0.5 \\ -0.5 \\ 0.5 \\ -0.5 \\
\end{bmatrix} =\begin{bmatrix}
1 \\ -1
\end{bmatrix} $$

$$ Wp_2=\begin{bmatrix}
1 & 0 & 0 & -1 \\
0 & 1 & -1 & 0 \\
\end{bmatrix}\begin{bmatrix}
0.5 \\ 0.5 \\ -0.5 \\ -0.5 \\
\end{bmatrix}=\begin{bmatrix}
1 \\ 1
\end{bmatrix} $$

네트워크 출력이 목표와 동일하다는 것을 알 수 있다.

예제 2) 입력 벡터가 직교하지 않을 때

$$ p_1=\begin{bmatrix}
1 \\ -1 \\ -1
\end{bmatrix},
p_2=\begin{bmatrix}
1 \\ 1 \\ -1
\end{bmatrix} $$

두 프로토타입 입력을 정규화하고 희망 출력을 -1과 1로 각각 선택하면 다음과 같다.

$$ p_1=\begin{bmatrix}
0.5774 \\ -0.5774 \\ -0.5774
\end{bmatrix}, t_1=\begin{bmatrix}
-1
\end{bmatrix} $$

$$ p_2=\begin{bmatrix}
0.5774 \\ 0.5774 \\ -0.5774
\end{bmatrix}, t_2=\begin{bmatrix}
1
\end{bmatrix} $$

가중치 행렬:

$$ W=TP^T=\begin{bmatrix}
-1 & 1
\end{bmatrix}\begin{bmatrix}
0.5774 & -0.5774 & -0.5774 \\
0.5774 & 0.5774 & -0.5774 \\
\end{bmatrix}=\begin{bmatrix}
1 & 1.1548 & 0
\end{bmatrix} $$

두 프로토타입 패턴을 가중치 행렬과 곱하면 다음과 같다.

$$ Wp_1=\begin{bmatrix}
0 & 1.1548 & 0
\end{bmatrix}\begin{bmatrix}
0.5774 \\ -0.5774 \\ -0.5774
\end{bmatrix} =\begin{bmatrix}
-0.6668
\end{bmatrix} $$

$$ Wp_2=\begin{bmatrix}
0 & 1.1548 & 0
\end{bmatrix}\begin{bmatrix}
0.5774 \\ 0.5774 \\ -0.5774
\end{bmatrix} =\begin{bmatrix}
0.6668
\end{bmatrix} $$

출력이 목표 출력과 일치하지 않는다.

학습 규칙 (learning rule) 은 네트워크의 가중치와 편향을 변경하는 방법을 의미한다. 학습 규칙은 크게

• 지도 학습 (supervised learning)
• 비지도 학습 (unsupervised learning)
• 강화 학습 (reinforcement learning)

으로 분류할 수 있다.

지도 학습은 훈련 집합 (training set) 과 같은 예시를 학습 규칙에 제공한다.

$$ \{p_1,t_1\}, \{p_2,t_2\}, ... , \{p_Q,t_Q\} $$

p는 네트워크 입력이며, t는 대응되는 정확한 출력 (목표) 이다.

1. 각 입력을 네트워크에 적용해서 네트워크 출력과 목표를 비교한다.
2. 네트워크 출력이 목표에 가까워지도록 학습 규칙을 사용해 네트워크의 가중치와 편향을 조정한다.

지도 학습에서 이진 분류로 결과가 나올 경우 그 출력을 discrete output 이라고 하며, classification problem 이 이에 해당한다. 시간의 흐름에 따라 값을 예측하는 경우 그 출력을 continuous output 이라고 하며, regression problem 이 이에 해당한다.

지도 학습은 훈련 알고리즘 (training algorithm) 에 네트워크 입력에 대한 목표를 제공하지만, 강화 학습은 등급 (또는 점수) 을 부여한다. 등급은 연속적인 입력에 대한 네트워크 성능 척도다. 강화 학습에는 액션에 따른 보상 (reward) 이 주어지며, 보상에 따라 액션을 바꿔가며 더 나은 결과를 유도한다.

비지도 학습은 사용 가능한 목표 출력이 없고, 네트워크 입력에 대한 반응만으로 가중치와 편향을 변경한다. 대부분의 비지도 학습 알고리즘은 군집화 연산을 수행해서 입력 패턴을 한정된 수의 클래스로 범주화 하도록 학습한다.

Moore-Penrose inverse of a matrix is the most widely known generalisation of the inverse matrix.

Note that the term 'generalised inverse' is sometimes used as a synonym for pseudopinverse.

History

The common uses of the pseudoinverse are

1. to compute a best-fit least squares solution to a system of linear equations that lacks a solution
2. to find the minimum Euclidean norm solution to a system of linear equations with multiple solutions

The Moore-Penrose pseudoinverse is defined for any matrix and is unique.

The Moore-Penrose pseudoinverse P+ of a matrix P satisfies the following properties:

When P has linearly independent columns, P+ can be computed as

This pseudoinverse is a left inverse that is:

Since P+ is injective, the multiplication of P+ and P is invertible.

• Note that 'injective' means that a function maps distinct elements to distinct outputs. no two elements of P+ map to the same element of P.

When P has linearly independent rows, P+ can be computed as

This is a right inverse as:

Since P+ is surjective, the multiplication of P and P+ is invertible.

• Note that 'surjective' means that a function maps every element of its domain to an element of its codomain. A surjective matrix maps every element of the column space of the matrix to an element of the space.

그람-슈미트 직교성 (Gram-Schmidt orthogonalization) 이해를 위한 개념

• 내적 (inner product): 두 벡터의 닮음 정도 (직각으로 갈수록 0에 가까워지고, 반대 방향의 경우 음수)
• 투영 (projection): 벡터 A에서 벡터 B로 직각 내렸을 때 (빛을 쏘면 어두워지는 영역을 생각하면 됨) A와 B가 맞닿는 벡터가 vector projection, 그 벡터의 길이가 scalar projection
• 놈 (norm): 기준점에서 한 벡터까지의 거리 (길이) 로서, 여러 놈이 있음
  • L0 norm: 길이를 나타내는 norm 의 개념이 아니라 vector 값 중 0이 아닌 값 개수
  • L1 norm: Manhattan distance 로 계산된 값
  • L2 norm: Euclidean distance 로 계산된 값으로, 같은 좌표가 주어졌을 때 L1 norm 보다 길이가 긴 편
  • L-infinity norm: max norm 이라고 불리며 vector 값 중 절대값이 가장 큰 값

두 벡터의 내적이 0 일 경우, 두 벡터는 직교한다.

벡터 A에 대한 직교 벡터 B를 구하는 방법은 벡터 A에서 벡터 A를 투영한 벡터를 빼면 된다.

위 그림은 연속된 벡터셋이 주어졌을 때 벡터 (Vk) 마다 직교하는 벡터 (Uk) 를 구하는 방법을 나타낸다.

식에 주어진 projection operator 는 위 그림과 같이 나타낼 수 있다. <> 표현은 내적을 뜻한다. 예를 들어 <U, U> 는 벡터 U와 벡터 U의 내적을, <V, U> 는 벡터 V와 벡터 U의 내적을 나타낸다. Uk와 무관한 'U'의 뜬금 없는 등장은 이 식이 연속된 벡터가 주어졌을 때 순서대로 직교성을 파악하기 위한 전개식으로, Uj의 j는 k-1으로 보면 된다.

직교화를 기하학적으로 생각하면 벡터 U 자신의 내적은 닮다 못해 아예 같이 때문에 최대 값이 될 거고, 이 값을 벡터 V와 벡터 U의 닮음 정도에 나누면 그 비율을 구할 수 있다. 이 비율을 벡터 U와 곱하면 비율만큼 길이에 변화가 생긴 벡터 U'가 나오게 되고, 이 U'가 바로 벡터 V와 직교하는 벡터가 된다.

그람-슈미트 직교화의 전 과정은 아래와 같다.

첫번째 직교벡터는 대상벡터로 지정하고, 두번째부터 projection operator 를 이용해 각 직교벡터를 구하면 된다.

예를 들어, 기저 벡터 집합 3개가 있다.

$$ y_1=\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}, y_2=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}, y_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix} $$

그람-슈미트 직교화를 이용해 직교 집합을 찾으려면

1단계:

$$ v_1=y_1=\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix} $$

2단계:

$$ v_2=y_2-\frac{v_1^Ty_2}{v_1^Tv_1}v_1=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}-\frac{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}}{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}=\begin{bmatrix}
1 \\ 0 \\ 0
\end{bmatrix}-\begin{bmatrix}
\frac{1}{3} \\ \frac{1}{3} \\ \frac{1}{3}
\end{bmatrix}=\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix} $$

3단계:

$$ v_3=y_3-\frac{V_1^Ty_3}{v_1^Rv_1}v_1-\frac{v_2^Ty_3}{v_2^Tv_2}v_2 $$

$$ v_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}-\frac{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}}{\begin{bmatrix}
1 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}}\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}-\frac{\begin{bmatrix}
2/3 & -1/3 & -1/3 \\
\end{bmatrix}\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}}{\begin{bmatrix}
2/3 & -1/3 & -1/3 \\
\end{bmatrix}\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix}}\begin{bmatrix}
2/3 \\ -1/3 \\ -1/3
\end{bmatrix} $$

$$ v_3=\begin{bmatrix}
0 \\ 1 \\ 0
\end{bmatrix}-\begin{bmatrix}
1/3 \\ 1/3 \\ 1/3
\end{bmatrix}-\begin{bmatrix}
-1/3 \\ 1/6 \\ 1/6
\end{bmatrix}=\begin{bmatrix}
0 \\ 1/3 \\ -1/3
\end{bmatrix} $$

이렇게 3단계로 구할 수 있다.